The Unit Circle (wrap-up)

After each class, I'm going to write up brief summaries and big take-aways from our Class Activities.

Converting between degrees and radians

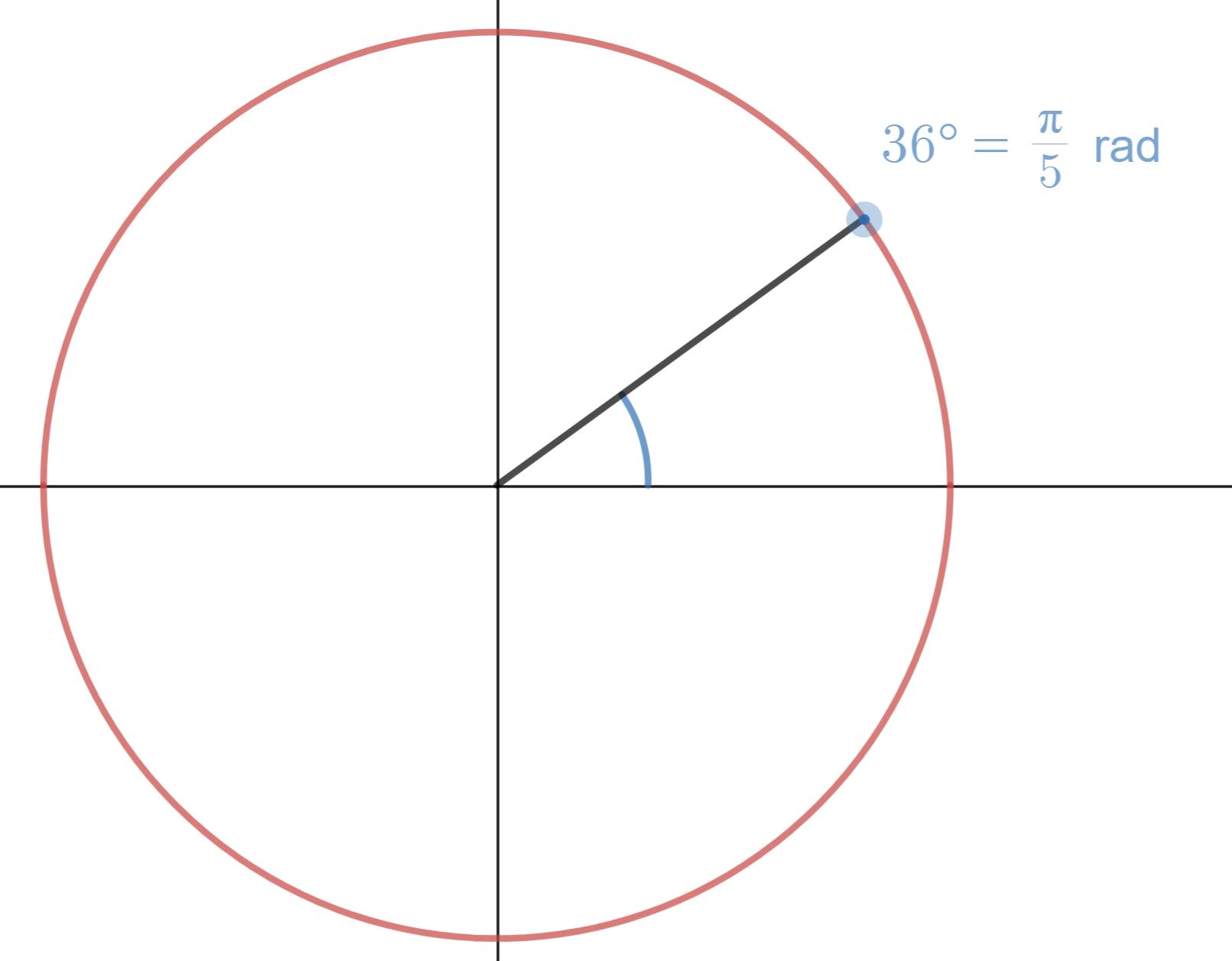
How many radians are in \(36^\circ\)?

There are a number of different ways you could go about this.

• You could notice that \(36^\circ\) is \(\tfrac{1}{10}\) of a circle, and a full circle is \(2\pi\) radians, so we have \(\tfrac{1}{10}(2\pi)=\tfrac{\pi}{5}\).
• You could set up a proportion, remembering that \(180^\circ\) is equivalent to \(\pi\) radians: \[ \begin{align*} \dfrac{36^\circ}{x\text{ rad}} &= \dfrac{180^\circ}{\pi\text{ rad}}\\ 36\pi &= 180x\\ x &= \dfrac{36\pi}{180}=\tfrac\pi5 \end{align*} \] You could have also had the right side as \(\dfrac{360^\circ}{2\pi}\), since both are equal to a full circle.
• You could think of it like a unit conversion or "dimensional analysis" problem like from chemistry: \[\dfrac{36^\circ}{1}\times\dfrac{\pi\text{ rad}}{180^\circ}=\tfrac\pi5\]

All of these really come down to thinking of angles as fractions of a circle.

How many degrees are in \(36\text{ rad}\)?

Again, we could solve this by setting up a proportion:

\[ \begin{align*} \dfrac{36\text{ rad}}{x^\circ} &= \dfrac{\pi\text{ rad}}{180^\circ}\\ 36\cdot 180 &= \pi x\\ x &= \tfrac{6480}{\pi} \approx 2062.64062 \end{align*} \]

Or we could do a unit conversion: \[\dfrac{36\text{ rad}}{1}\times\dfrac{180^\circ}{\pi\text{ rad}}=\tfrac{6480}{\pi}\]

In the end, there is a "formulaic" way of thinking about these:

To convert degrees to radians, multiply by \(\dfrac{\pi}{180}\).

To convert radians to degrees, multiply by \(\dfrac{180}{\pi}\).

But memorizing formulas will only get you so far — what makes it stick is understanding why they work. That way you can fall back on any of the above methods even if you forget the formula (or forget which one is which).

Converting between degrees and radians

Are \(-1773^\circ\) and \(1467^\circ\) coterminal angles?

I was impressed by the variety of ways I saw in class!

• You could start with \(-1773^\circ\) and repeatedly add \(360^\circ\) to see if you get to \(1467^\circ\). (You do, so they are coterminal.)
• You could divide each by \(360^\circ\) which shows that each one is a little more than four full circles (\(1440^\circ\)) in some direction. Then, get rid of those full circles: \[ \begin{align*} 1467^\circ - 1440^\circ &= 27^\circ\\ -1773^\circ +1440^\circ &=-333^\circ \end{align*} \] Since \(27^\circ\) and \(-333^\circ\) are coterminal angles, so are our original two. (You can see this by adding another \(360^\circ\) to the negative angle.)
• You could look at the difference between the angles: \[1647^\circ-(-1773^\circ)=3240^\circ=9\cdot 360^\circ\] Since the angles are nine full circles apart — a whole number of full circles — the angles are coterminal.

Are \(2.85\pi\) and \(3.85\pi\) coterminal angles?

Again this has to do with whether the two angles are some number of full circles apart, but this time we're in radians, so a full circle is \(2\pi\) radians.

You can try any of the above methods, but you should find that these two angles are not coterminal — in fact, they're on exact opposite sides of the circle, half a circle away from each other.

As you can see, we will repeatedly be using the fact that a full circle is \(360^\circ\) or \(2\pi\) radians. That equivalence will be so ingrained in you before long that you'll see it in your sleep!

---

Return to MAT 130 main page

Posted by Bill Shillito