The Law of Cosines

Return to MAT 130 main page

Go to Preview Activity

---

Textbook Reference: Section 8.2 Non-right Triangles: Law of Cosines

---

Have you ever wished you could use the Pythagorean Theorem, but then you realized you couldn't because you didn't have a right triangle?

The Law of Cosines is what you needed.

The Law of Cosines states that the three sides of any triangle are related by the following relationship: \[{\color{flatred}c}^2={\color{flatblue}a}^2+{\color{flatpurple}b}^2-2{\color{flatblue}a}{\color{flatpurple}b}\cos({\color{flatred}C})\] Notice that this looks remarkably like the Pythagorean Theorem, but with a "fudge factor" of \(-2{\color{flatblue}a}{\color{flatpurple}b}\cos({\color{flatred}C})\) to make it work for any triangle, not just right triangles.

This means that there's nothing particularly special about having \({\color{flatred}c}\) on the left side! We could just as easily have \({\color{flatblue}a}\) be the focus of the formula: \[{\color{flatblue}a}^2={\color{flatpurple}b}^2+{\color{flatred}c}^2-2{\color{flatpurple}b}{\color{flatred}c}\cos({\color{flatblue}A})\] Or \({\color{flatpurple}b}\): \[{\color{flatpurple}b}^2={\color{flatblue}a}^2+{\color{flatred}c}^2-2{\color{flatblue}a}{\color{flatred}c}\cos({\color{flatpurple}B})\]

The proof of the Law of Cosines is actually very similar to the proof of the Law of Sines, and you can expand the box below to read it if you'd like.

Proof: Law of Cosines

Let's just prove for now that \({\color{flatred}c}^2={\color{flatblue}a}^2+{\color{flatpurple}b}^2-2{\color{flatblue}a}{\color{flatpurple}b}\cos({\color{flatred}C})\).

Just like in the proof of Law of Cosines, we'll drop an altitude of length \(h\) from point \(\color{flatpurple}B\) as follows:

However, this time we'll also split \(\color{flatpurple}b\) into two quantities \(\color{flatgreen}x\) and \(\color{flatpink}b-x\).

Since we have two right triangles, we can use the Pythagorean Theorem on both: \[h^2+{\color{flatpink}(b-x)}^2={\color{flatred}c}^2\qquad\qquad h^2+{\color{flatgreen}x}^2={\color{flatblue}a}^2\] Since \(h^2\) shows up in both, we can solve for it in each equation: \[h^2={\color{flatred}c}^2-{\color{flatpink}(b-x)}^2\qquad\qquad h^2={\color{flatblue}a}^2-{\color{flatgreen}x}^2\] Both expressions equal \(h^2\), so they must equal each other: \[{{\color{flatred}c}^2-{\color{flatpink}(b-x)}^2=\color{flatblue}a}^2-{\color{flatgreen}x}^2\] Get \(c^2\) by itself: \[{{\color{flatred}c}^2=\color{flatblue}a}^2-{\color{flatgreen}x}^2+{\color{flatpink}(b-x)}^2\] Now let's expand the \({\color{flatpink}(b-x)}^2\): \[{{\color{flatred}c}^2=\color{flatblue}a}^2-{\color{flatgreen}x}^2+{\color{flatpurple}b}^2-2{\color{flatpurple}b}{\color{flatgreen}x}+{\color{flatgreen}x}^2\] Well what do you know — those \({\color{flatgreen}x}^2\)'s will cancel out! \[{{\color{flatred}c}^2=\color{flatblue}a}^2+{\color{flatpurple}b}^2-2{\color{flatpurple}b}{\color{flatgreen}x}\] We're almost there. All that's left is to use SOH-CAH-TOA to notice that \(\cos({\color{flatred}C})=\dfrac{\color{flatgreen}x}{\color{flatblue}a}\), so \({\color{flatgreen}x}={\color{flatblue}a}\cos({\color{flatred}C})\). Making the appropriate substitution we finally get: \[{\color{flatred}c}^2={\color{flatblue}a}^2+{\color{flatpurple}b}^2-2{\color{flatblue}a}{\color{flatpurple}b}\cos({\color{flatred}C})\] This proves the first version of the Law of Cosines. We could prove the other two versions by turning the triangle on its side and dropping altitudes from \(\color{flatblue}A\) or \(\color{flatred}C\), so at this point we're done! \(\blacksquare\)

Example

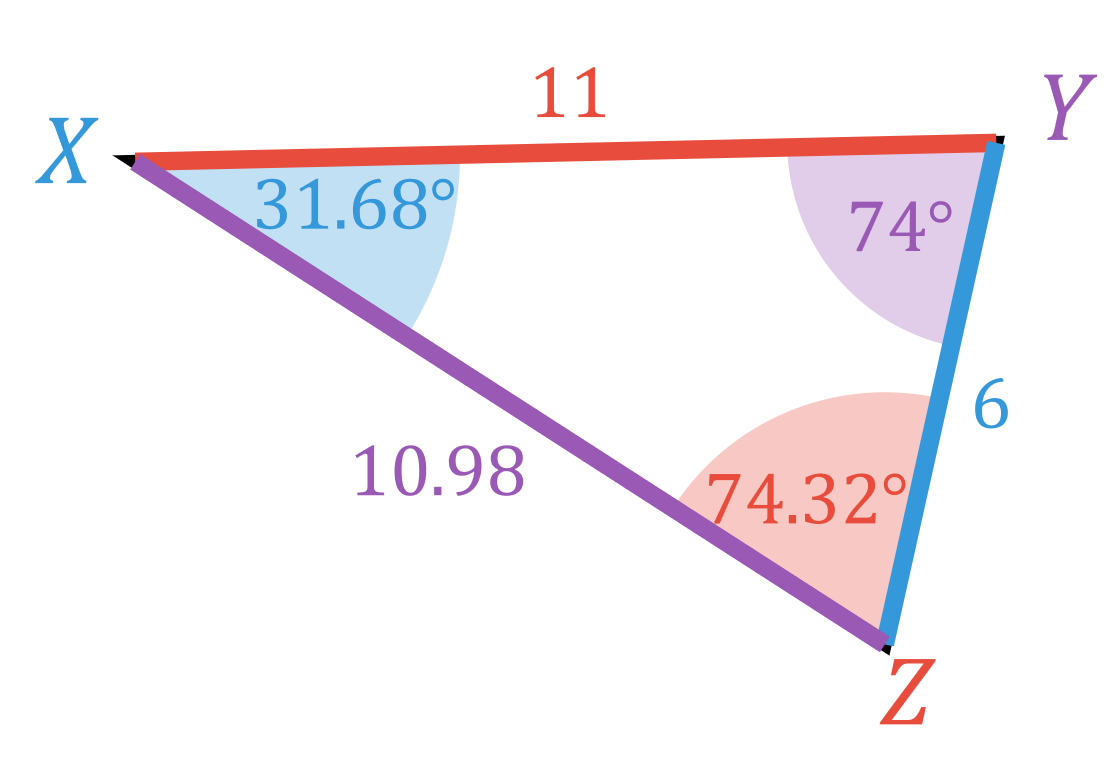
Suppose we have triangle \({\color{flatblue}X}{\color{flatpurple}Y}{\color{flatred}Z}\) in the figure below:

Notice that we can't use the Law of Sines to solve this triangle (why?), so we need to use the Law of Cosines instead.

We know angle \(\color{flatpurple}Y\), so we can find side \(\color{flatpurple}y\) by making it the focus of our formula: \[{\color{flatpurple}y}^2={\color{flatblue}x}^2+{\color{flatred}z}^2-2{\color{flatblue}x}{\color{flatred}z}\cos({\color{flatpurple}Y})\] Then we can plug in the information we have: \[{\color{flatpurple}y}^2={\color{flatblue}6}^2+{\color{flatred}11}^2-2\cdot{\color{flatblue}6}\cdot{\color{flatred}11}\cdot\cos({\color{flatpurple}74^\circ})\] Evaluating this on a calculator gives \(\color{flatpurple}y^2\approx 120.615869\), so taking the square root we have \(\color{flatpurple}y\approx 10.982525\).\( \DeclareMathOperator{\Sin}{Sin} \DeclareMathOperator{\Cos}{Cos} \DeclareMathOperator{\Tan}{Tan} \DeclareMathOperator{\Csc}{Csc} \DeclareMathOperator{\Sec}{Sec} \DeclareMathOperator{\Cot}{Cot} \DeclareMathOperator{\Arcsin}{Arcsin} \DeclareMathOperator{\Arccos}{Arccos} \DeclareMathOperator{\Arctan}{Arctan} \DeclareMathOperator{\Arccsc}{Arccsc} \DeclareMathOperator{\Arcsec}{Arcsec} \DeclareMathOperator{\Arccot}{Arccot} \)

And hey, now that we know both \(\color{flatpurple}y\) and \(\color{flatpurple}Y\), we can use the Law of Sines! \[ \begin{align*} \dfrac{\color{flatblue}x}{\sin({\color{flatblue}X})} &= \dfrac{\color{flatpurple}y}{\sin({\color{flatpurple}Y})}\\ \dfrac{\color{flatblue}6}{\sin({\color{flatblue}X})} &= \dfrac{\color{flatpurple}10.98}{\sin({\color{flatpurple}74^\circ})}\\ {\color{flatpurple}10.98}\sin({\color{flatblue}X}) &= {\color{flatblue}6}\sin({\color{flatpurple}74^\circ})\\ \sin({\color{flatblue}X}) &= \dfrac{{\color{flatblue}6}\sin({\color{flatpurple}74^\circ})}{\color{flatpurple}10.98}\\ {\color{flatblue}X} &= \Sin^{-1}\left(\dfrac{{\color{flatblue}6}\sin(\color{flatpurple}{74^\circ})}{\color{flatpurple}10.98}\right)\\ {\color{flatblue}X} &\approx {31.68^\circ} \end{align*} \] And finally subtracting our two known angles from \(180^\circ\), we find that the last angle is \(\color{flatred}Z\approx 74.32^\circ\), so the triangle is solved.

---

Preview Activity 13

Answer these questions and submit your answers as a document on Moodle. (Please submit as .docx or .pdf if possible.)

1. Solve the following triangle.
   
   
2. Suppose a triangle has sides of length \(6\), \(7\), and \(11\). Find the measures of all the angles; include a sketch to show which angle is across from which side.
3. Take another look at the first version of the Law of Cosines: \[{\color{flatred}c}^2={\color{flatblue}a}^2+{\color{flatpurple}b}^2-2{\color{flatblue}a}{\color{flatpurple}b}\cos({\color{flatred}C})\] Suppose \(\color{flatred}C=90^\circ\). What does \(\cos({\color{flatred}C})\) come out to? What does this do to the formula?
4. Answer AT LEAST one of the following questions:
   1. What was something you found interesting about this activity?
   2. What was an "a-ha" moment you had while doing this activity?
   3. What was the muddiest point of this activity for you?
   4. What question(s) do you have about anything you've done?

Answers

---

Return to MAT 130 main page

Posted by Bill Shillito